Logistische Regression

Die logistische Regression ist ein wichtiger und häufig verwendeter Algorithmus in Statistik und Data Science. Noch besser: du kannst ihn in R ganz einfach implementieren. Der Algorithmus trifft Vorhersagen über die Wahrscheinlichkeit eines bestimmten Ereignisses und kommt deshalb bei Klassifikationsproblemen zum Einsatz. Es ist wie die lineare Regression ein Supervised Learning-Algorithmus. Supervised Learning ist eine Methode des maschinellen Lernens, bei der ein Algorithmus anhand bekannter Labels (y-Werte) trainiert wird, um Vorhersagen für neue, unbekannte Daten zu treffen. In diesem Post behandle ich die klassische logistische Regression, die für binäre Zielvariablen eingesetzt wird, genauer gesagt also „binäre logistische Regression“. Typische Anwendungsbereiche für diese sind z.B. die Einstufung einer E-mail, (spam oder nicht), die Diagnose von Tumoren (bösartig oder gutartig), oder die Prognose, ob ein Kunde bald ein Abo kündigen wird (customer churn). 

Die logistische Regression basiert auf dem Konzept des Logit-Modells, bei dem die Wahrscheinlichkeit eines bestimmten Ereignisses als Funktion der unabhängigen Variablen modelliert wird. Die logistische Funktion führt dabei zu einer S-förmigen Kurve zwischen 0 und 1, die die Wahrscheinlichkeit der Klassenzugehörigkeit für jeden Wert der unabhängigen Variablen vorhersagt. In R kannst du ein solches Modell mit einem einzigen Befehl erstellen und interpretieren, und genau das schauen wir uns jetzt an!

Warum Logistische Regression?

Warum kann man nicht einfach eine lineare Regression verwenden? Nun, die logistische Regression ist notwendig, weil sie speziell für Probleme entwickelt wurde, bei denen die Zielgröße kategorial oder binär ist. Im Gegensatz dazu ist die lineare Regression für Probleme geeignet, bei denen die Vorhersagevariablen numerisch sind. Bei der logistischen Regression wird eine logistische Funktion („logit“) verwendet, welche zu einer S-förmigen Kurve führt und nur Werte zwischen 0 und 1 zulässt. Und somit ist sie perfekt für binäre Zielvariablen – denn Werte zwischen 0 und 1 lassen sich wunderbar als Wahrscheinlichkeiten interpretieren.

Im folgenden Beispiel erstellen wir einen synthetischen Datensatz mit zwei Variablen: score und subscribed. Wir nehmen an, dass Personen, bei denen ein bestimmtes Merkmal (score) höher ausgeprägt ist, eher ein Abo abschließen (subscribed). Letzteres wäre somit unsere Zielgröße, „y“. Wir schauen uns nun an, warum eine lineare Regression für diesen Fall nicht gut geeignet ist.

Beispiel

library(data.table)
library(ggplot2)

dt <- data.table(score = sort(runif(50, 0, 1)))
dt[, subscribed := rbinom(.N, 1, score)]

ggplot(dt, aes(score, subscribed)) + geom_point(size=2) + 
  theme_minimal() + xlim(c(0,1)) + ylim(c(0,1))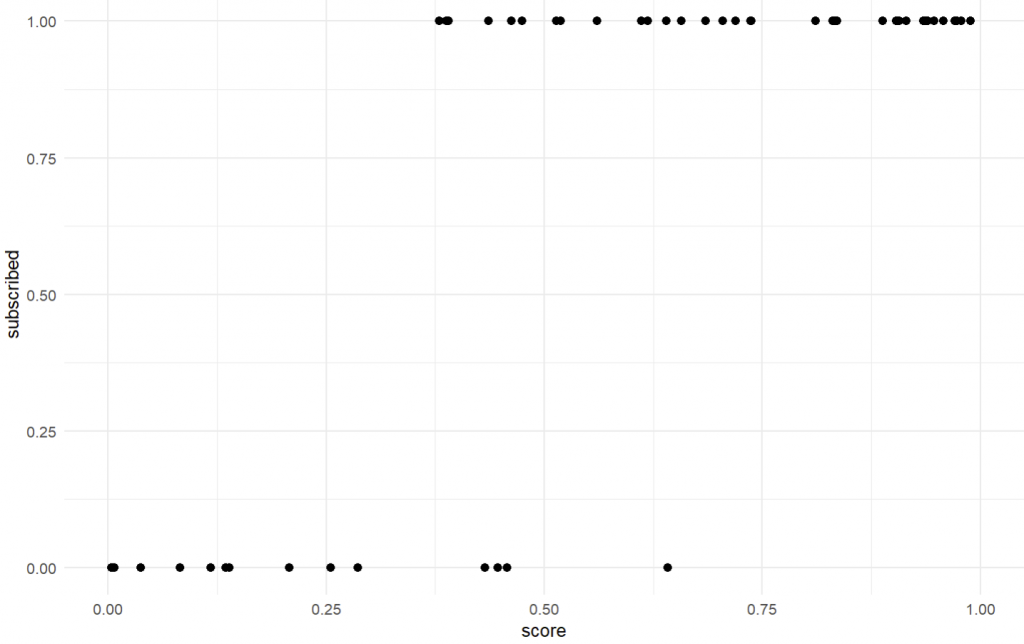

Anschließend erstellen wir ein Regressionsmodell mit der lm-Funktion. Wir speichern auch die vorhergesagten Werte mit predict(mdl) und die Residuen mit residuals(mdl).

mdl <- lm(subscribed ~ score, data=dt)
dt[, pre := predict(mdl)]
dt[, res := residuals(mdl)]

Anschließend können wir uns den x-Wert berechnen, welcher genau zu einem y-Wert von 0.5 führt. Dies tun wir, weil wir unseren threshold auf 0.5 setzen – bei einem Wert über 0.5 würden wir y = 1 vermuten; bei einem Wert unter 0.5 entsprechend y = 0. Die mathematische Gleichung wäre also 0.5 = b0 + b1*score und wir lösen nach score auf. Somit ist score = (0.5 - b0) / b1. Anschließend plotten wir alles mit ggplot.

score_thresh <- (0.5 - mdl$coefficients[1]) / mdl$coefficients[2]
ggplot(dt, aes(score, subscribed)) + geom_point(size=2) + 
  geom_line(aes(score, pre), color="darkorange") +
  geom_hline(yintercept=0.5, color="steelblue", linetype="dashed") +
  geom_vline(xintercept=score_thresh, color="steelblue", linetype="dashed") +
  theme_minimal() + xlim(c(0,1)) + ylim(c(0,1))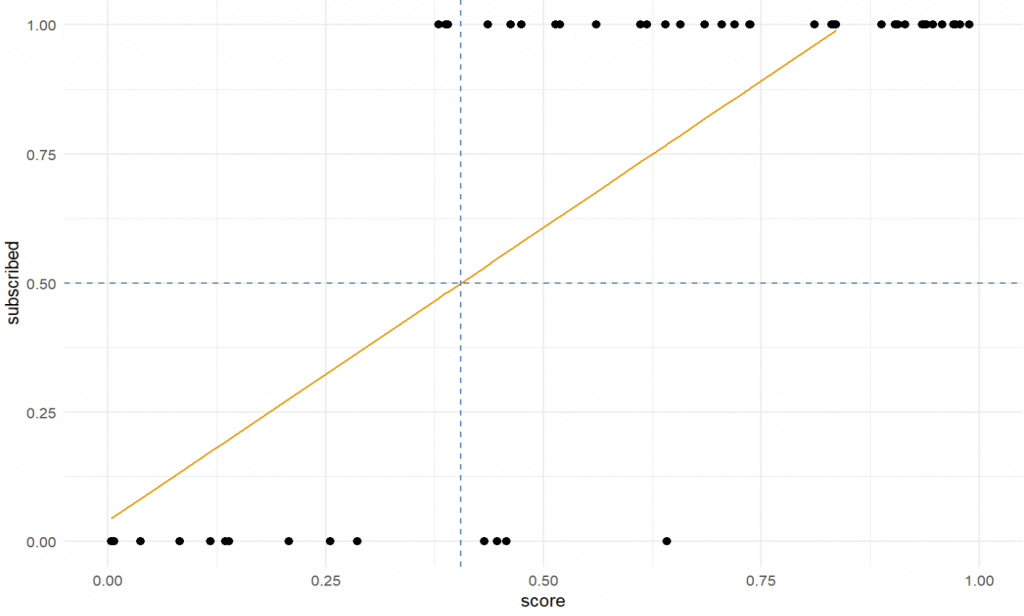

So weit, so gut. Doch nun kommen die Probleme, vor allem:

• Was ist mit den Annahmen für eine lineare Regression (Linearität, Normalität und Heteroskedastizität)?
• Was bedeuten vorhergesagte Werte unter 0 oder über 1? Als Wahrscheinlichkeiten lassen die sich ja nicht interpretieren.

Schauen wir uns den ersten Punkt als Plots an (Code hier mal weggelassen, unten ist der gesamte Code):

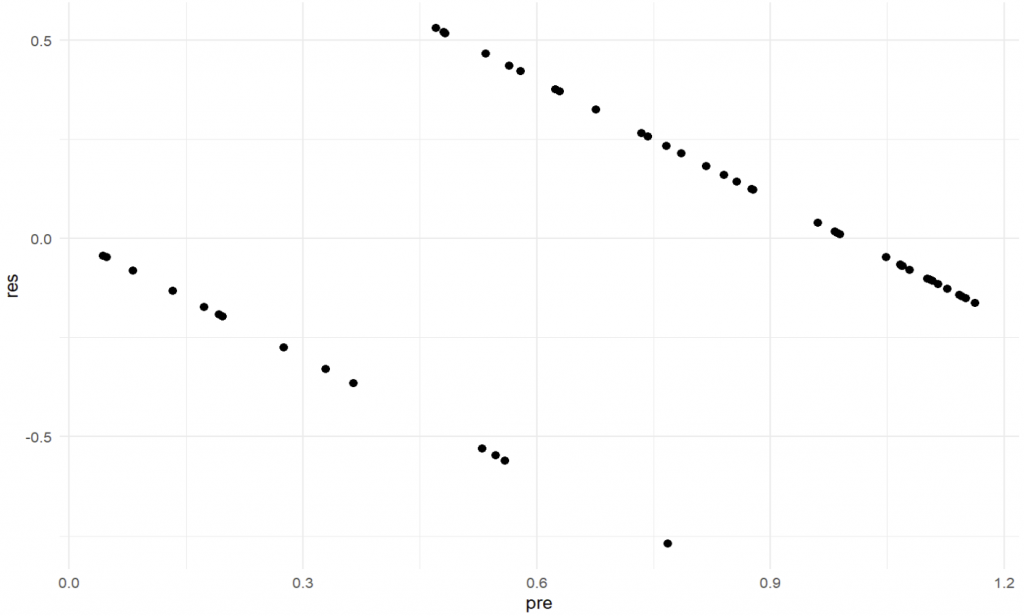
(Annahme der Linearität – sieht nicht gut aus!)

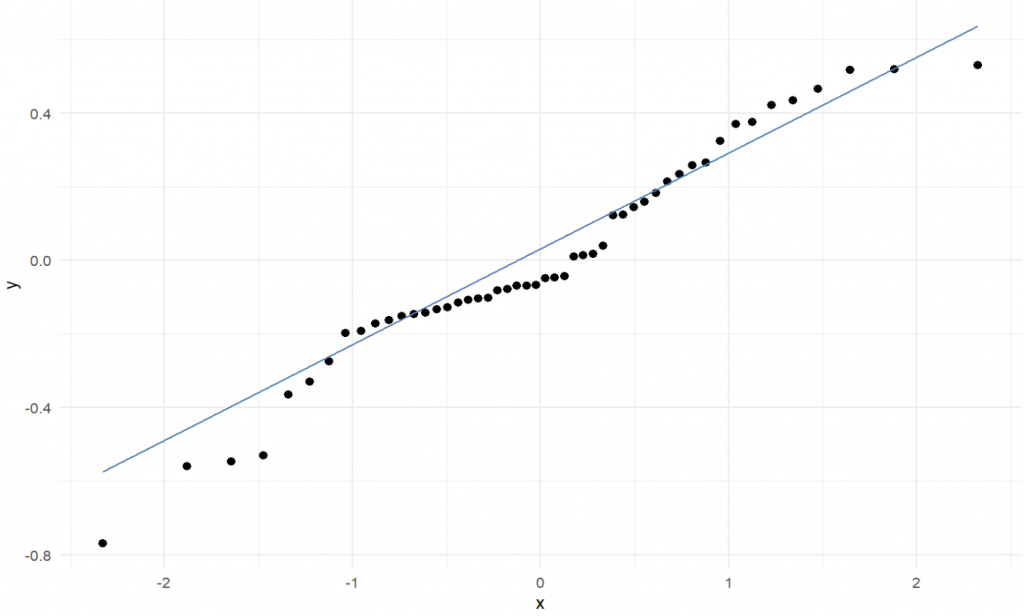
(Annahme der Normalität der Residuen (QQ-Plot) – könnte auch besser sein)

Logistische Regression in R

Nun schauen wir, wie es besser geht. Um eine logistische Regression in R zu berechnen, verwenden wir die Funktion glm (für „generalized linear models“) und nutzen für den Parameter family den String „binomial“. Wir berechnen wieder die vorhergesagten Werte und schauen uns die Zusammenfassung an.

mdl_logistic <- glm(subscribed ~ score, data=dt, family=binomial)
dt[, pre_logistic := predict(mdl_logistic, type="response")]
summary(mdl_logistic)

Die typische S-Kurve können wir nun im Plot erkennen.

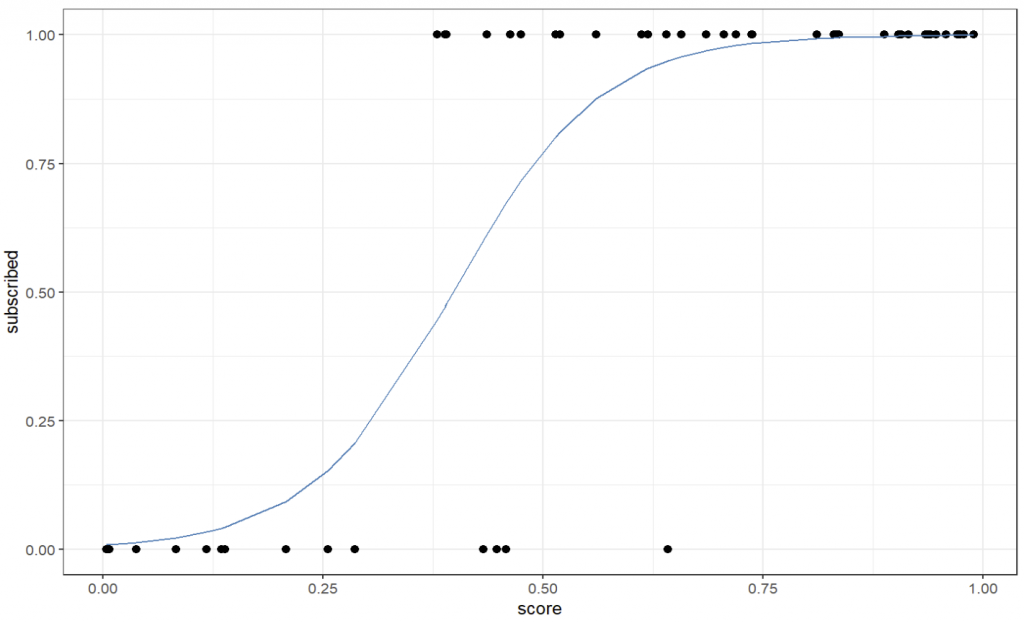
Letzte Anmerkungen

Dieser Post soll eine kleine Einführung in die logistische Regression in R sein. Somit sind tiefergehende mathematisch / statistische Erklärungen bewusst weggelassen. Dennoch ein paar Hinweise:

• Das logistische Modell ist ein nichtlineares Modell und somit gelten andere Regeln, was Interpretation und Annahmen angeht. So gibt es z.B. kein R² als Indikator für erklärte Varianz, sondern nur ein „pseudo-R²“.
• Ebenso ist die Interpretation der Koeffizienten unterschiedlich. Folgendes kann man sich aber merken: Ein positiver Koeffizient bedeutet, dass eine Erhöhung der Variablen zu einer höheren Wahrscheinlichkeit von y = 1 führt.
• In diesem Beispiel gab es nur einen Prädiktor scores; natürlich lassen sich beliebig viele Prädiktoren hinzufügen.
• Es gibt nichtlineare Modelle, welche mehrere Kategorien zulassen, sog. multinomiale logistische Regressionen.

Das wars für heute. Wenn du weitere Fragen oder Anmerkungen hast, kommentiere gerne oder schreib eine E-Mail.

Viel Erfolg!